Exercice 1

1.On donne $A =\dfrac{2}{3} −\sqrt{3}$ et $B = − \dfrac{6 + 9\sqrt{3}}{23}$∙

Montre que $A$ et $B$ sont inverses.

2.On considère les réels $E, F$ et $G$ suivants : $E=\sqrt{3}−1 , F=\sqrt{\sqrt{3}−1}$ et $G=(\sqrt{3}−1)^{2}$.

Sans utiliser la calculatrice, range, avec justification à l’appui, ces trois nombres dans l’ordre croissant.

3.On pose $K=\dfrac{1+\dfrac{1}{2}}{1−\dfrac{1}{2}}∶ \dfrac{1−\dfrac{2}{3}}{1+\dfrac{2}{3}}$∙

Montre que $K$ est un entier.

4.On pose : $L= \dfrac{(a^{−2}b^{3})2×(ab^{3})^{−4}}{b×(a^{3}b^{2})^{−3}}$ où $a$ et $b$ sont deux réels non nuls.

Ecris $L$ sous la forme $L=a^{m}×b^{p}$ où $m$ et $p$ sont des entiers relatifs.

Exercice 2

Soit $ABC$ un triangle rectangle en $A$ tel que : $AB=4$ et $BC=5$.

On considère trois points $E,F$ et $K$ du plan, tels que :
$\vec{AE}=2\vec{AC}+\vec{AB}; \vec{BF}=2\vec{BC}; \vec{AK}=2\vec{AC}$

1.Construis le triangle $ABC$, puis place les points $E,F$ et $K$.

2.Montre que :

a)Les points $E,F$ et $K$ sont alignés.

b)Le point $K$ est le milieu du segment $[EF]$.

3.Quelle est la nature du quadrilatère$ BKFA$ ? Justifie ta réponse.

4.Calcule le rayon du cercle circonscrit au triangle $BEF$.

Exercice 3

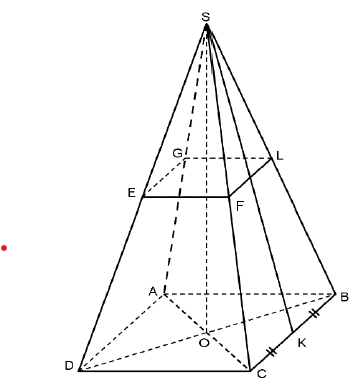La figure à gauche est une pyramide régulière $SABCD$ de sommet $S$, de hauteur $SO=20$.

Le quadrilatère $EFLG$ est une section de la pyramide $SABCD$ par un plan parallèle au plan de la base $ABCD$.

On suppose que $AD =8$ et $\dfrac{GF}{AC}=\dfrac{1}{2}$ et on admettra que les droits $(GF)$ et $(AC)$ sont parallèles.

1.Montre que $SC= 12\sqrt{3}$ et $SK= 4\sqrt{26}$ .

2.a) Calcule l’aire latérale de la pyramide $SABCD$ .

b) Déduis-en l’aire latérale $AL$ de la pyramide $SGLFE$.

3.Calcule le volume de la pyramide $SABCD$ .

4.Déduis-en le volume du solide $ABCDGLFE$ .