FONCTION LOGARITHME NEPERIEN
I. Etude de la fonction logarithme népérien
1. Définition et notation
La fonction logarithme népérien notée ln est la fonction définie et dérivable $\left]0; +\infty\right[$ qui s'annule en $1$ et qui
a pour fonction dérivée la fonction définie par $\dfrac{1}{x}$.
Autrement dit :
$\bullet$ L'ensemble de définition de la fonction $ln$ est$\left]0; +\infty\right[$ et pour tout $x\neq\left]0; +\infty\right[$ ,l'image de $x$ par la fonction népérien est le réel noté $ln x$
$\bullet ln 1=0$.
$\bullet$La fonction $ln$ est dérivable sur sur $\left]0; +\infty\right[$ et pour tout $x>0$, on a $(ln)'(x)=\dfrac{1}{x}$.
2. Propriétés :
Si$a>0$ et $b>0$ et alors on a :
(propriété fondamentale)
$ln\left(\dfrac{1}{a}\right)=ln a$
$ln\left(\dfrac{a}{b}\right)=ln a-ln b$.
Pour tout nombre rationnel $r,ln a^{r}=r ln a$
$ln\sqrt{a}\dfrac{1}{2}ln a$
Remarque
$\dfrac{ln a}{ln b}\neq ln a -ln b$
$(ln a)^{r}\neq r ln a$
Exemple :Exprimons à l'aide de $ln 2$ et $ln 3$ , le nombre suivant :
$ln(2\times 3)ln\dfrac{1}{3}ln2^{3}=ln\dfrac{3}{2}$
3. Représentation graphique de $ln$
Soit $f$ la fonction définie par $f(x)=ln x$
$\bullet D_{f}=\left]0;+\infty\right[$
$\bullet$ Limites aux bornes de :$D_{f}$.
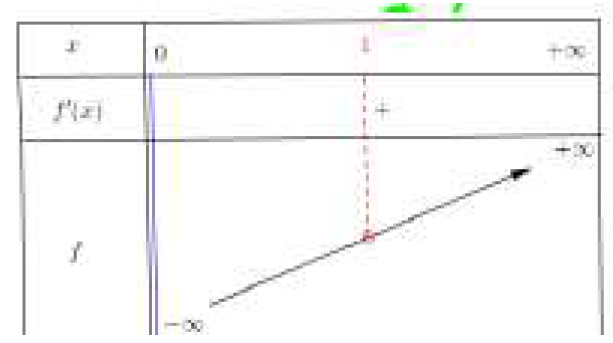
$\lim\limits_{x\longrightarrow \,0^{+}}f(x)=\lim\limits_{x\longrightarrow \,0^{+}}ln x=-\infty$
$\lim\limits_{x\longrightarrow \,+\infty}f(x)=\lim\limits_{x\longrightarrow \,0^{+}}ln x=+\infty$
$\bullet$ Branches infinies
$\lim\limits_{x\longrightarrow\,0^{+}}f(x)=-\infty$ donc la droite d'équation $x=0$
est une asymptote verticale de$C_{f}$
$\lim\limits_{x\longrightarrow\,-\infty}\dfrac{f(x)}{x}=\lim\limits_{x\longrightarrow \,-\infty}\dfrac{ln x}{x}=0$ donc l'axe des abscisse est une branche parabolique se $C_{f}$en $+\infty$.
$\bullet$ Tableau de variation
Pour tout $x\neq \left]0 ;\infty\right[,f'(x)=(ln)'(x)=\dfrac{1}{x}$ or $\dfrac{1}{x}>0$ sur $\left]0 ;\infty\right[$ donc $f$ est strictement
croissante sur $\left]0 ;\infty\right[$ .
$\bullet$ Remarque
Il existe un unique $e\in\left]0 ;\infty\right[$;ln e=1$ réel noté e tel que ; $e$
est $e\approx 2,718$.
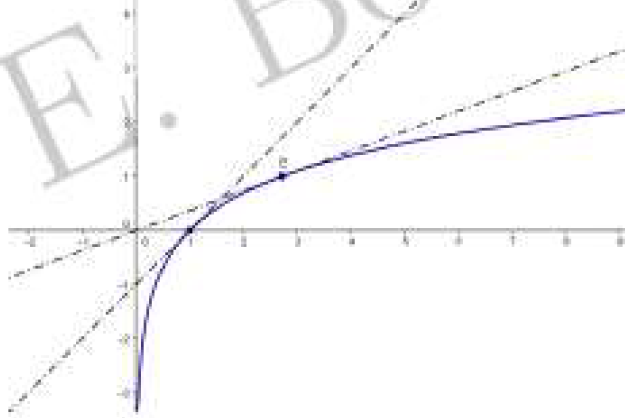
Courbe représentative de $ln$
L'équation de la tangente aux points d'abscisses $1$
et $e$
L'équation de la tangente $(T')$ à $C_{f}$
à au point d'abscisse $1$ est $(T):y=f'(1)(x-1)+f(1)=(x-1)$
.
L'équation de la tangente $(T')$ à $C_{f}$
à au point d'abscisse $(T):y=f'(e)(x-e)+f(e)=\dfrac{1}{e}(x-e)+1=dfrac{1}{e}x$
Tableau de valeurs
$$\begin{array}{|c|c|c|c|c|c|}
\hline
x& 1& e& 4& 5& 6\\
\hline
ln x& 0& 1& 1,4& 1,6& 1,8\\
\hline
\end{array}$$
Courbe
II. Equations et inéquations faisant intervenir ln
1. Equations
$\bullet$ Propriété
Si$a>0$ et $b>0$ alors on a :$ln(a)= ln(b)\Leftrightarrow a=b$
$\bullet$ Equation du type $ln(u(x))\leq ln(v(x))$
On résout le systéme d'inéquation $$\left\lbrace\begin{array}{rcl}
u(x)&>&0\\
v(x)&>&0
\end{array}\right.$$.L'ensemble des solutions de ce systéme est appelé domaine de validité de l'équation équation et est noté $D_{v}$
Dans $D_{v}$ l'équation $ln(u(x))\leq ln(v(x))$ devient $u(x)=v(x)$.
Ainsi on résout
dans $D_{v}$ équation $u(x)=v(x)$.
$\bullet$ Exemple :
Résolvons dans $\mathbb{R}$ équation $ln(-x+1)=ln(2x+6)$
2. Inéquations
$\bullet$ Propriété
Si $a>0$ et $b>0$ alors on a :
$ln(a)\leq ln(b)\Leftrightarrow a\leq b$
$ln(a)\leq ln(b)\Leftrightarrow a\geq b$
NB : Dans chacun des cas ci-dessus, les inégalités larges peuvent être remplacées par des
inégalités strictes.
Inéquation du type $ln(u(x))\leq ln(v(x))$
Pour résoudre une telle inéquation, on procède ainsi :
On détermine $D_{v}$ en résolvant le système $$\left\lbrace\begin{array}{rcl}
u(x)&>&0\\
v(x)&>&0
\end{array}\right.$$
Dans $D_{v}$ inéquation $ln(u(x))\leq ln(v(x))$ devient $u(x))\leq v(x))$
Ainsi on résout
inéquation $u(x))\leq v(x))$ dont l'ensemble des solutions sera notée $S_{1}$.
L'ensemble des solutions $S$ de l'équation est donnée par $S=S_{1}\cap D_{v}$
Exemple :
Résolvons dans $\mathbb{R}$, inéquation $ln(2x-1)\leq ln(x+1)$
Nb : Pour résoudre une inéquation du type ,$ln(u(x))\geq ln(v(x))$ on procède de la
même manière mais en remplaçant par$\leq par\geq$ .
III. Fonctions faisant intervenir $ln$
1. Limites usuelles
$\lim\limits_{x\longrightarrow \,0^{+}}xln x)=0 $
Si $n$ est un entier naturel
non nul alors $\lim\limits_{x\longrightarrow \,0^{+}}ln x)=0 $
2. Ensemble de définition
Soit $u$ une fonction et $f$ la fonction définie par $f(x)=ln\left[u(x)\right]$ .
$f(x)$ existe ssi existe et $u(x)>0$
$\bullet$Exemple
Déterminons l'ensemble définition de la fonction $f$ tel que $f(x)=left(\dfrac{x+1}{x-1}$
3. Limites de $ln\left[ u(x)\right]$.
Pour calculer $\lim\limits_{x\longrightarrow \,a}ln\left[ u(x)\right]$,on calcule d'abord $\lim\limits_{x\longrightarrow\,a}u(x)$
Si $\lim\limits_{x\longrightarrow\,a}u(x)=b$ avec $b>0$ alors
$\lim\limits_{x\longrightarrow\,a}ln\left[ u(x)\right]=ln b$
Si $\lim\limits_{x\longrightarrow\,a}u(x)=0$ alors $\lim\limits_{x\longrightarrow\,a}ln\left[ u(x)\right]=-\infty$
Si $\lim\limits_{x\longrightarrow\,a}u(x)=+\infty$ alors $\lim\limits_{x\longrightarrow\,a}ln\left[ u(x)\right]=+\infty$
Exemple : calculons les limites suivantes
$\lim\limits_{x\longrightarrow\,+\infty}ln\left(\dfrac{2x+1}{x-1}\right)$
$\lim\limits_{x\longrightarrow\,+\infty}ln\left(\dfrac{x+1}{x^{2}+1}\right)$
$\lim\limits_{x\longrightarrow\, 0}ln\left(\dfrac{1}{x^{2}}\right)=$
4. Dérivée
Si $f(x)=ln\left[u(x)\right]$ alors $f'(x)=ln'\left[u(x)\right]=\dfrac{u'(x)}{u(x)}$
$\bullet$ Exemple
$f(x)=ln\left(x^{x}+x-6\right)$.
Calculons $f'(x)$ .
Commentaires
HighRollerMage (non vérifié)
dim, 10/19/2025 - 14:44
Permalien
Telegram 1win
https://t.me/s/official_1win_aviator
ChipWhisperer (non vérifié)
mar, 10/28/2025 - 14:25
Permalien
Промокоды и фриспины в одном месте — подписал и забыл искать
https://t.me/s/Beefcasino_rus/32
AceSorcerer (non vérifié)
jeu, 10/30/2025 - 02:54
Permalien
Рабочие промокоды: коротко и по делу
https://t.me/Best_promocode_rus/550
RouletteRogue (non vérifié)
ven, 10/31/2025 - 00:06
Permalien
Где взять действующие промокоды на слоты, live и crash
https://t.me/s/Beefcasino_rus/57
AllInAce (non vérifié)
sam, 11/01/2025 - 01:28
Permalien
Канал с рабочими промокодами: экономит время
https://t.me/s/Beefcasino_rus/59
LuckyBandit (non vérifié)
dim, 11/02/2025 - 04:36
Permalien
1WIN - telegram
https://t.me/s/official_1win_aviator/43
Angeltriat (non vérifié)
mar, 11/11/2025 - 19:50
Permalien
1xbet
https://t.me/va_1xbet/6
AdrianKique (non vérifié)
sam, 11/15/2025 - 09:49
Permalien
1xbet
https://t.me/rq_1xbet/1203
JoshuaWoday (non vérifié)
sam, 11/15/2025 - 13:16
Permalien
1xbet
https://t.me/s/rq_1xbet/1412
JoshuaWoday (non vérifié)
sam, 11/15/2025 - 14:53
Permalien
1xbet
https://t.me/s/rq_1xbet/720
JoshuaWoday (non vérifié)
sam, 11/15/2025 - 16:33
Permalien
1xbet
https://t.me/s/rq_1xbet/1398
JoshuaWoday (non vérifié)
sam, 11/15/2025 - 18:15
Permalien
1xbet
https://t.me/s/rq_1xbet/828
CharlesAssek (non vérifié)
mer, 11/19/2025 - 20:39
Permalien
Рейтинг казино
https://t.me/s/top_online_kazino/9
TerrySat (non vérifié)
jeu, 11/20/2025 - 09:31
Permalien
1xbet
http://images.google.gp/url?q=https://t.me/s/Official_1xbet_1xbet/1209
TerrySat (non vérifié)
jeu, 11/20/2025 - 11:11
Permalien
1xbet
https://www.google.cz/url?sa=t&url=https://t.me/Official_1xbet_1xbet/805
TerrySat (non vérifié)
jeu, 11/20/2025 - 12:53
Permalien
1xbet
https://maps.google.ad/url?q=https://t.me/Official_1xbet_1xbet/389
WilliamNus (non vérifié)
jeu, 11/20/2025 - 13:02
Permalien
Аппаратный маникюр и педикюр с покрытием
https://www.avito.ru/surgut/predlozheniya_uslug/apparatnyy_manikyur_i_pe...
TerrySat (non vérifié)
jeu, 11/20/2025 - 14:42
Permalien
1xbet
http://maps.google.com.gi/url?q=https://t.me/Official_1xbet_1xbet/634
TerrySat (non vérifié)
jeu, 11/20/2025 - 16:35
Permalien
1xbet
https://cse.google.com.my/url?sa=t&url=https://t.me/Official_1xbet_1xbet...
TerrySat (non vérifié)
jeu, 11/20/2025 - 18:17
Permalien
1xbet
https://images.google.com.ni/url?sa=t&url=https://t.me/Official_1xbet_1x...
DealerShadow (non vérifié)
ven, 11/21/2025 - 11:11
Permalien
1WIN - telegram
https://t.me/of_1xbet/739
Joshuatal (non vérifié)
ven, 11/21/2025 - 15:41
Permalien
1win
<a href="https://t.me/s/bz_1win">1 вин контакты</a> — свяжитесь уже сейчас и получите мгновенный доступ к лучшим онлайн-казино и ставкам на спорт! Пользуйтесь фриспинами, бонусами за депозит до 500%, высокими коэффициентами и быстрой выплатой выигрышей, выполняйте ставки в лайв-режиме и выводите средства за считанные минуты — всё это возможно с удобным личным кабинетом и круглосуточной поддержкой.
Joshuatal (non vérifié)
ven, 11/21/2025 - 21:28
Permalien
1win
Развлекайся и выигрывай с <a href="https://t.me/s/bz_1win">1win pro ru</a> — получи бонусы до 10 000 ? за первый депозит и фриспины для слот-машин! Делай ставки на спорт с высокими коэффициентами и участвуй в лайв-ставках круглосуточно, выводи выигрыш быстро и без комиссий. В личном кабинете доступны кэшбэк до 15%, быстрый вывод средств и уникальные промокоды — всё для твоего реального выигрыша и удобства!
Joshuatal (non vérifié)
sam, 11/22/2025 - 02:53
Permalien
1win
Выигрывайте с <a href="https://t.me/s/bz_1win">win 8 1 exe</a> и погрузитесь в мир онлайн казино и ставок на спорт! Получите до 100% бонуса за депозит, фриспины и высокие коэффициенты на лайв-ставки — все это доступно через личный кабинет 1win. Быстрые выплаты, минимальный депозит и круглосуточная поддержка делают игру выгодной и максимально комфортной.
Joshuatal (non vérifié)
sam, 11/22/2025 - 08:15
Permalien
1win
<a href="https://t.me/s/bz_1win">1вин рун</a> — начни прямо сейчас и получи бонус до 10 000? и 150 фриспинов за первый депозит! Играй в онлайн-казино и ставки на спорт с высокими коэффициентами, делай лайв-ставки и выигрывай реальный кэш — быстрый вывод денег, кэшбэк до 5% и персональный личный кабинет всегда под рукой. От минимального депозита 300? до круглосуточной поддержки и мгновенных выплат — всё для твоего победного опыта!
Pokerdomquist (non vérifié)
mar, 12/02/2025 - 03:40
Permalien
Pokerdom
https://t.me/officials_pokerdom/3164
AceSorcerer (non vérifié)
ven, 12/05/2025 - 17:10
Permalien
iGaming play
https://t.me/iGaming_live/4869
beefcasino (non vérifié)
dim, 12/07/2025 - 10:53
Permalien
Beef casino
https://t.me/s/Beefcasino_officials
beefcasino (non vérifié)
dim, 12/07/2025 - 12:48
Permalien
Beef casino
https://t.me/s/Beefcasino_officials
Ajouter un commentaire