Composition du premier semestre 1 S1

Exercice 1(08 points)

ABC est un triangle du plan tel que : AB = 4cm , AC = 5cm et \(\cos ((\widehat{A})=\frac{3}{5}\).

    1. Construire le triangle \(ABC\) sans chercher une valeur approchée de l’angle \(\widehat{BAC}\) et expliquer la méthode utilisée. $\quad (1~\text{pt})$
    2. \(A'\) est le milieu de \([BC]\) et \(I\) est le barycentre des points pondérés \((A,2),(B,-1),(C,1)\).
    
        a. Démontrer que \(AA'CI\) est un parallélogramme. $\quad (0.5~\text{pt})$
        b. Définir \(I\) comme barycentre des points \(A, A', B, C\) affectés des coefficients dont la somme est 1. $\quad (0.5~\text{pt})$
    
    3. Calculer \(BC, AA', \cos(\widehat{ACB})\) et \(IC\) (\(4 \times 0.5~\text{pt}\))
    4. Déterminer et construire :
    
        a. L’ensemble \(E_1\) des points \(M\) du plan tels que \(\dfrac{MA}{MB} = 2\)  $(1~\text{pt})$
        b. L’ensemble \(E_2\) des points \(M\) du plan tels que \(\vec{AB} \cdot (2\vec{MA} - \vec{MB} + \vec{MC}) = -16\) $\quad (1~\text{pt})$
    
    5. Pour tout point \(M\) du plan, on pose \(f(M) = \vec{CM} \cdot (2\vec{MA} + \vec{MC})\).
    
        a. Calculer \(f(A), f(B), f(C), f(I)\)  (\(4 \times 0.25~\text{pt}\))
        b. Déterminer pour tout réel \(k\) la ligne de niveau \(k\) de \(f\) $\quad (0.75~\text{pt})$
        c. Construire la ligne de niveau passant par \(A\) $\quad (0.25~\text{pt})$
    

Exercice 2 (5 points)

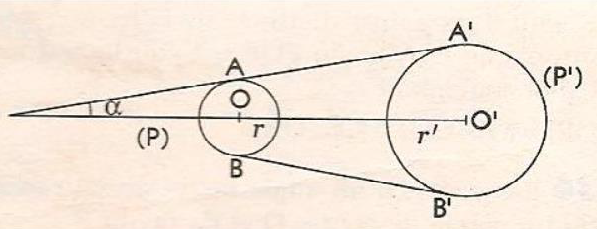
Une chaîne de vélo s’enroule autour d’un pignon \((P)\) de centre \(O\) et de rayon \(r\) et d’un pédalier \((P')\) de centre \(O'\) et de rayon \(r'\). On pose \(OO' = d\). Soit \(\alpha\) la mesure de l’angle que fait \((OO')\) avec \((AA')\), tangente commune extérieure à \((P)\) et \((P')\).

    1. Montrer que \(\sin \alpha = \dfrac{r' - r}{d}\). $\quad (0.75~\text{pt})$
    2. Exprimer \(\cos 2\alpha\) en fonction de \(\sin \alpha\) et déduire que 
    \[
    \cos 2\alpha = \dfrac{d^2 - 2(r' - r)^2}{d^2}. \quad (2 \times 0.5~\text{pt})
    \]
    3. On se propose de calculer la longueur \(L\) de la chaîne. Soit \(A\) et \(B\) (resp. \(A'\) et \(B'\)) les points de contact de la chaîne avec \((P)\) (resp. \((P')\)).
    
        a. Montrer que \(AA' = d \cos \alpha\). $\quad (0.5~\text{pt})$
        b. Montrer que \(\widehat{AOB} = \widehat{A'O'B'} = \pi - 2\alpha\). \quad (\(2 \times 0.5~\text{pt}\))
        c. En déduire, en fonction de \(\alpha, r, r'\), la longueur de l’arc \(\widehat{AB}\) puis montrer que
        \[
        L = 2d \cos \alpha + \pi(r' + r) + 2\alpha(r' - r). \quad (0.75~\text{pt})
        \]
    
    4. Application : \(r = 5\ \text{cm}, r' = 10\ \text{cm}, d = 45\ \text{cm}\). Calculer une valeur approchée à \(10^{-2}\) de \(\alpha\) et \(L\). \quad (\(2 \times 0.5~\text{pt}\))

Exercice 3 (7 points)

     Calculer les limites suivantes :
    
       a.  \(\lim_{x \to 0} \dfrac{\sqrt{x + 3} - \sqrt{4x + 3}}{\sqrt{x + 4} - \sqrt{2x + 4}}\) $\quad$  b. \(\lim_{x \to 8} \dfrac{\sqrt[3]{x} - 2}{\sqrt{x + 19} - 3}\)  \( \quad 2 \times 0.75~\text{pt}\)
       c. \(\lim_{x \to 0} \dfrac{x(1 - \cos x)}{\sin 3x - 3 \sin x}\) $\quad$ d. \(\lim_{x \to \dfrac{\pi}{3}} \dfrac{\tan x \tan\left(x - \dfrac{\pi}{3}\right)}{1 - 2 \cos x}\)  \( \quad 2 \times 0.75~\text{pt}\)
       e. \(\lim_{x \to 2} \dfrac{2 - \sqrt{x^2 - 4x + 8}}{x - 2} \sin\left(\dfrac{1}{x - 2}\right)\) $\quad$ f. \(\lim_{x \to 0} \sin\left[x E\left(\dfrac{\pi}{x}\right)\right]\)  \(\quad 2 \times 0.75~\text{pt}\)
    
    2. On considère les fonctions \(f_m\) et \(g_m\) définies par :
    \[
    g_m(x) = \dfrac{(m^2 - m)x^2 + 2mx + 1}{(m - 1)x^2 + x - 2}, \quad f_m(x) = \sqrt{x^2 + x + 1} - mx.
    \]
    Discuter suivant les valeurs du paramètre \(m\) la limite en \(+\infty\) et \(-\infty\) de \(f_m\) et \(g_m\). $\quad (2.5~\text{pt})$